Observação: Por motivos didáticos, neste texto nos limitaremos a vetores no plano \(\mathbb{R}^{2}\).
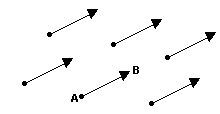Um segmento AB é caracterizado pelos pontos A e B. Se especificarmos quais desses dois pontos é o ponto inicial e qual é o ponto final, teremos um segmento orientado AB. Podemos dizer, nesse caso, que A é a origem e B a extremidade do segmento.
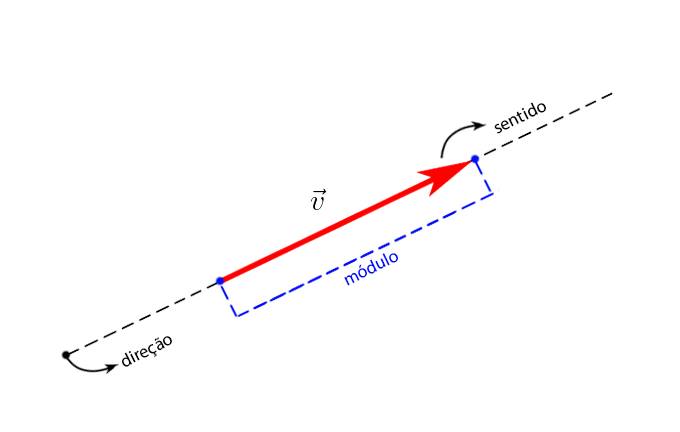
Denota-se vetor o conjunto de segmentos orientados equipolentes a AB, ou seja, possuem mesma direção, sentido e módulo de AB. Cada segmento de reta orientado do grupo será um representante do vetor \(\vec{AB}\).
Ou seja, quando dois segmentos orientados são equipolentes (possuem mesma direção, sentido e módulo) dizemos que estes determinam um único vetor.
Na física, esses objetos matemáticos são de extrema importância e podem ser definidos como uma representação geométrica de uma determinada grandeza, sendo capaz de indicar sua direção e sentido. Ou seja, eles foram criados para podermos estudar de forma simples e objetiva as grandezas vetoriais.
Mas o que seria uma grandeza vetorial? Bem, às vezes, saber o valor de uma determinada grandeza não é o suficiente para se ter uma perfeita compreensão do que está acontecendo. Nesses casos, é necessária também uma orientação. Logo, uma grandeza vetorial é aquela que, como mencionado acima, possui direção, sentido e módulo, diferente de uma grandeza escalar, que não “aponta” para lugar algum (massa, tempo, temperatura e etc.). Podemos citar como exemplos de grandeza vetorial a velocidade com que uma partícula se move, o deslocamento total de um automóvel ou a aceleração de um corpo qualquer.
Temos aqui um exemplo de vetor velocidade.
Componentes de um vetor
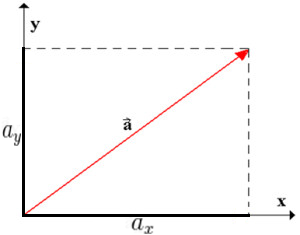
Para facilitar o estudo de um vetor faz-se uso de componentes vetoriais, que nada mais são do que a representação do vetor em eixos de um plano cartesiano, processo também conhecido como decomposição de vetor.
Neste caso, podemos observar que as componentes do vetor \(\vec{a}\) nos eixos x e y são, respectivamente, \({a}_x\) e \({a}_y\) .
Podemos determinar geometricamente as componentes do vetor a partir do triângulo retângulo formado na figura.
Sendo \(\theta\) o ângulo formado entre \(\vec{a}\) e o eixo x, temos que: $$\cos\theta=\frac{{a}_x}{\left | \vec a \right |}$$ e $$\sin\theta=\frac{{a}_y}{\left | \vec a \right |}$$
Então, $${a}_x=\left | \vec a \right |\cos\theta$$ $${a}_y=\left | \vec a \right |\sin\theta$$
Da mesma forma que podemos determinar as componentes de um vetor através desses cálculos simples, podemos também determinar o módulo do vetor através de suas componentes. Para encontrar o módulo faz-se uso da equação abaixo, que nada mais é do que o conhecido Teorema de Pitágoras: $$|\vec a|=\sqrt{(a_x)^{2}+(a_y)^{2}} $$
Já o ângulo \(\theta\), podemos obtê-lo através da simples relação:
$$\tan\theta=\frac{{a}_y}{{a}_x}$$
Revisão do Texto
Professor Dr. André Correia Riserio do Bonfim
Bibliografias e Pesquisas
- “Fundamentos da Física; Mecânica; 1” – Halliday & Resnick
Energia e Potência
Queda Livre
Can I copy and save the images? It seems that the format is quite unfamiliar. Perhaps, there’s a link to them saved separately in the archive? Would appreciate.
yeah, i wish i can copy and save the images
Play the most popular and outstanding game spades with all unlocked level without any download and app installation and you should have not to pay any amount to play the spades on our homepage.
Great post,Thanks for providing us this great knowledge,Keep it up.
great article, I was very impressed about it, wish you would have stayed next share
Thanx for sharing such useful post keep it up
The article you share here is great. I really like and appreciate your work
Thanks for sharing this news with us.
That’s great information I was looking for, can you share more about it.
A fantastic likelihood to me and it also would have been a superb expertise to view this web site. Hard to get such informative web site or web site. I possess several devices and having a solid idea of these people did wonders and effort continues to be seeing for this web site.
It is difficult to find a website or website that is so informative. My possession of many gadgets, together with the fact that I have a thorough understanding of these individuals, has worked miracles, and I am continuing to put in effort for this website.
Waffle unlimited is a hot word game. Different from the daily version. Waffle offers an unlimited version that you can play until you get bored. Your task is based on the characters given in the box.
Olá a todos, gostaria de chamar sua atenção para a Casa de Apostas porque ela é a melhor opção para todos os jogadores brasileiros. Suas avaliações de casas de apostas não são apenas um conjunto de frases gerais, mas informações claras e concisas que realmente o ajudam a fazer a escolha certa. Gostei do fato de que é possível encontrar avaliações não apenas das casas de apostas mais populares, mas também de plataformas menos conhecidas, mas ainda assim lucrativas. A Casa de Apostas é um verdadeiro guia para qualquer apostador no Brasil!
Thank you for this informative article. It has answered many of my questions about the topic. Much appreciated!
VideoShow Pro Activated
Thanks for the valuable information. This post was very well-written.
Appreciate the depth of knowledge in this article. Well done!
This article has provided me with a lot of answers to my queries regarding the subject, and I am grateful for it.
geometry dash wave
Hi, my friend, I’m here
Your article is incredibly insightful and thought-provoking.
he way you presented complex information so simply is remarkable.
This post was a great read. Very informative and interesting.
Componentes de um vetor
Para facilitar o estudo de um vetor faz-se uso de componentes vetoriais, que nada mais são do que a representação do vetor em eixos de um plano cartesiano, processo também conhecido como decomposição de vetor.