Observação: Embora seja possível definir espaços vetoriais complexos (onde os escalares são números complexos), serão estudados em nossos posts apenas espaços vetoriais reais, onde os escalares são números reais.
Soma de vetores
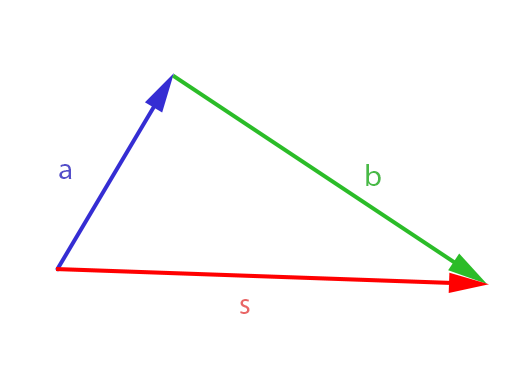
Consideremos uma formiga que se moveu de a até b e, em seguida, de b até c. Seu deslocamento pode ser representado com apenas dois vetores, um seguido do outro. Mas, para simplificar, podemos representar seu deslocamento total de uma outra maneira, com um único vetor \(\vec s\), denominado vetor soma ou vetor resultante.
Consideremos aqui \(\vec s\) o vetor soma de \(\vec a\) e \(\vec b\). Logo, \(\vec a +\vec b=\vec s\).
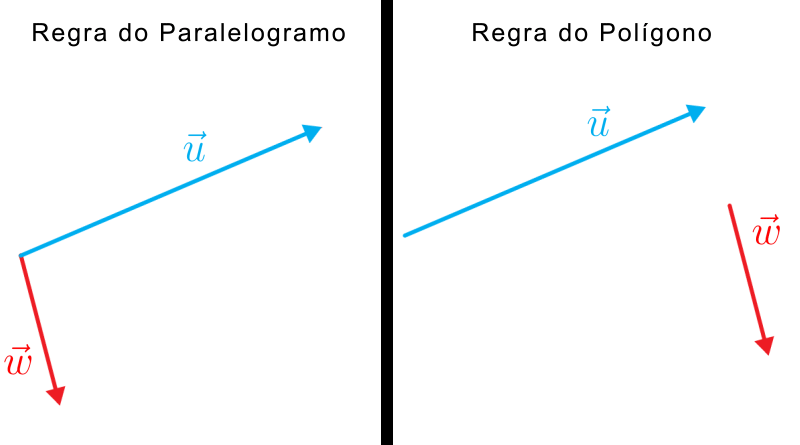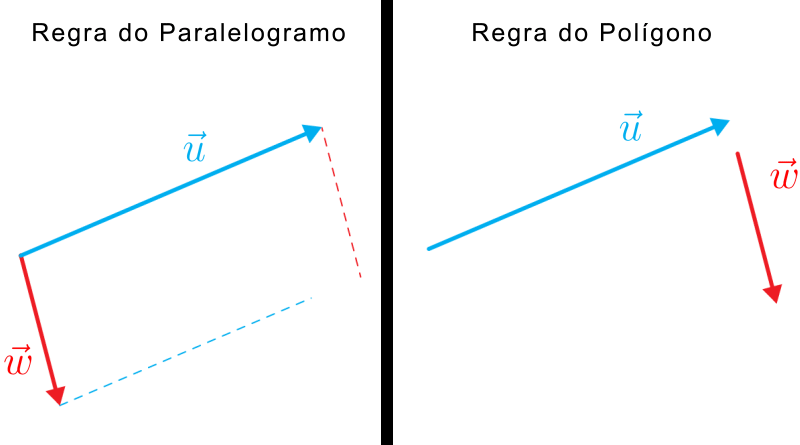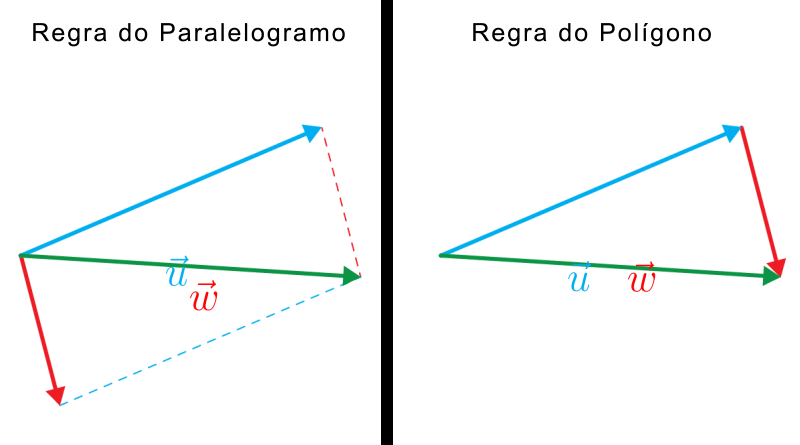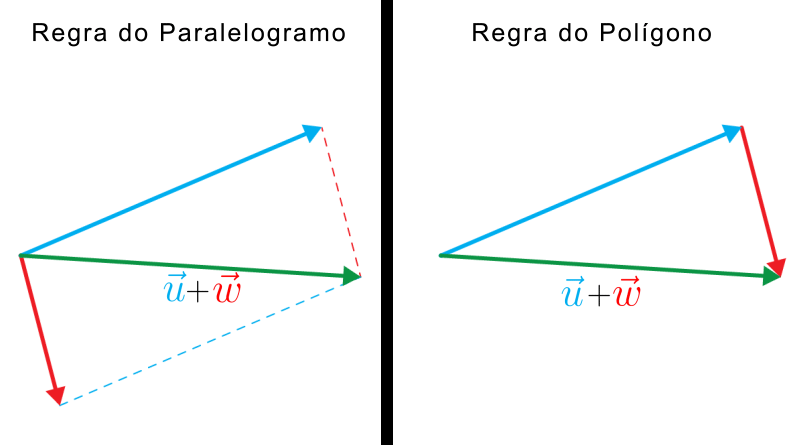
Diferente da soma algébrica comum, na soma de vetores o módulo e orientação também estão envolvidos na operação. Existem duas formas diferentes para realização da soma de vetores, elas são conhecidas como regra do polígono e regra do paralelogramo. Vejamos como utilizá-las:
Regra do Polígono
Se trata de um método simples para efetuar a adição de vetores e está representado na imagem acima. Tendo dois vetores não-nulos, devemos desenhar o \(\vec a\) no ângulo apropriado e o \(b\), também no ângulo correto, com sua origem na extremidade de \(\vec a\). O vetor soma seria o vetor que liga a origem de um dos vetores a extremidade do outro. No caso da imagem o vetor soma é \(\vec s\).
A lei de comutatividade e associatividade (clique no box abaixo para saber o que são elas) são válidas para a soma entre vetores. Ou seja, a ordem em que os vetores são somados é irrelevante. Logo, \( \vec a+ \vec b = \vec b + \vec a\). Quando existem mais de dois vetores, podemos colocá-los em qualquer ordem para somá-los.
Lei comutativa:
Durante a multiplicação ou adição de dois ou mais fatores, se a ordem destes for alterada o resultado continuará sendo o mesmo. Por exemplo, \(a+b = b+a\).
Ex: $$4+2=2+4=6$$
Lei associativa:
Ao associarmos parcelas, o resultado da operação permanece inalterado. Ou seja, \((a+b)+c=a+(b+c)\).
Ex: $$(5+4)+2=5+(4+2)=11$$
Ambas as propriedades são válidas para vetores. Logo, se tratando da lei comutativa, temos que: \(\vec a + \vec b = \vec b + \vec c\). Observe a animação:
E essa é a lei associativa aplicada em vetores: \((\vec a + \vec b) + \vec c = \vec a + (\vec b + \vec c)\). Veja o exemplo onde temos o vetor amarelo como resultante:
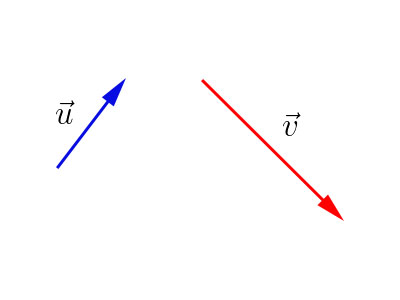
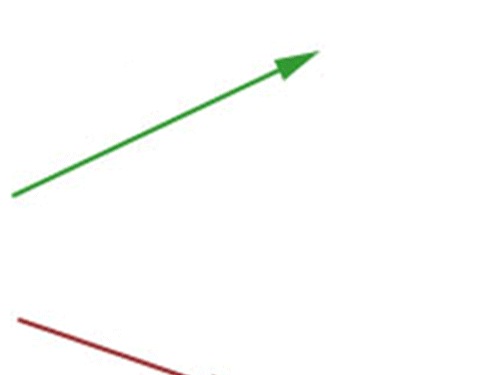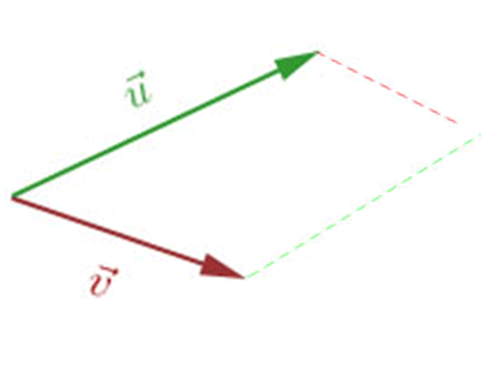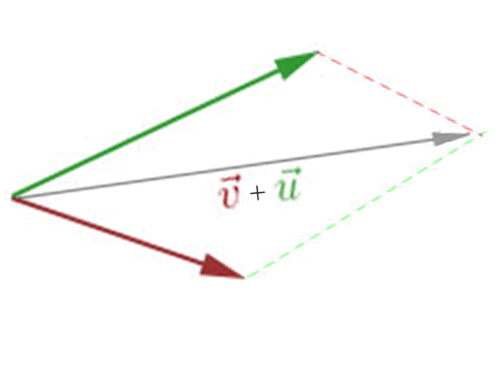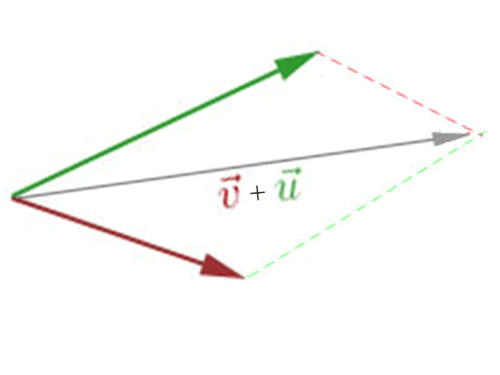
Vejamos esse segundo exemplo. Temos aqui dois vetores, \(\vec u\) e \(\vec v\):
Ao somá-los, obtemos o seguinte vetor soma:
Ou seja, posicionamos a extremidade de \(\vec u\) junto a origem de \(\vec v\) e como vetor resultante temos \(\vec u + \vec v\).
Essa regra também é válida para quando temos três ou mais vetores. Por exemplo:
Fazendo uso da regra do polígono chegamos ao seguinte resultado:
Regra do Paralelogramo
Sejam \(\vec u\) e \(\vec v\) dois vetores, ao somá-los, para determinarmos o módulo, sentido e direção do vetor resultante, devemos desenhar o paralelogramo definido por eles. Vejamos um exemplo com os vetores \(\vec u\) e \(\vec v\):
Traçamos retas paralelas aos vetores e ligamos uma a outra. Logo em seguida, desenhamos uma reta “no centro” do paralelogramo, obtendo, assim, o vetor resultante. Observe:
Através das animações abaixo podemos ver que, independente da regra usada (regra do polígono ou do paralelogramo), o resultado será sempre o mesmo:
Multiplicação de um vetor por um escalar
Multiplicação de vetor por um escalar é, como o próprio nome já diz, o produto entre um vetor e um número qualquer. Se temos o vetor \(\vec u\) sendo multiplicado por um escalar a, o produto será a\(\vec u\).
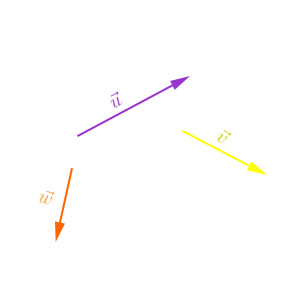
Esses são alguns exemplos de multiplicação de vetor por um escalar:
No terceiro exemplo, onde o \(\vec w\) está sendo multiplicado por 0, o vetor resultante “desaparece”. Esse é o chamado vetor nulo, ou seja, ele não possui dimensão, não tem um módulo, uma direção e nem um sentido.
Se a\(\neq 0\) e \(\vec u \neq 0\), o vetor resultante terá direção igual a de \(\vec u\), comprimento igual ao módulo de a vezes o comprimento de \(\vec u\), ou seja, \(\left |a \vec u \right |= \left | a \right |\left | \vec u \right |\) e o sentido será o mesmo de \(\vec u\) se a for positivo e sentido oposto ao de \(\vec u\) se a for negativo.
Bibliografia e Pesquisas
- “Fundamentos da Física; Mecânica; 1” – Halliday & Resnick
- “Vetores e Uma iniciação à Geometria Analítica – Mello e Watanabe”
- “Vetores e Escalares – Prof. Romero Tavares da Silva”



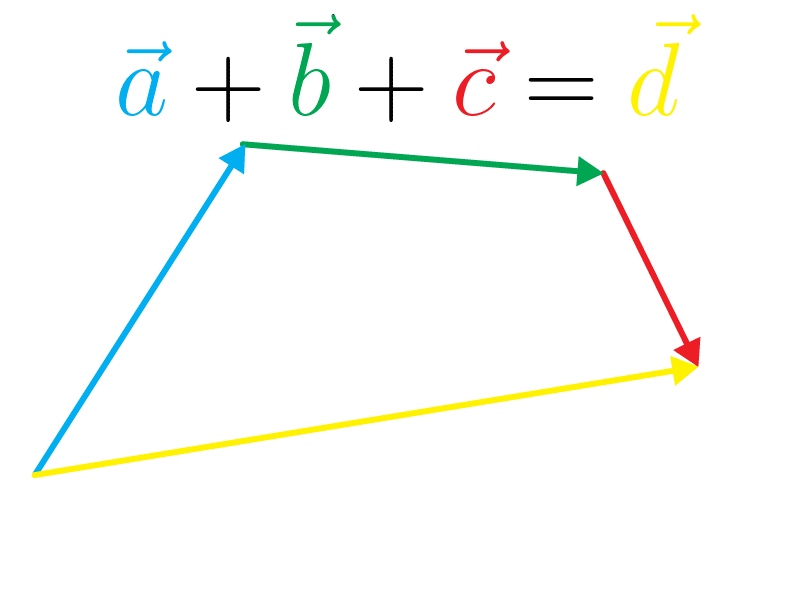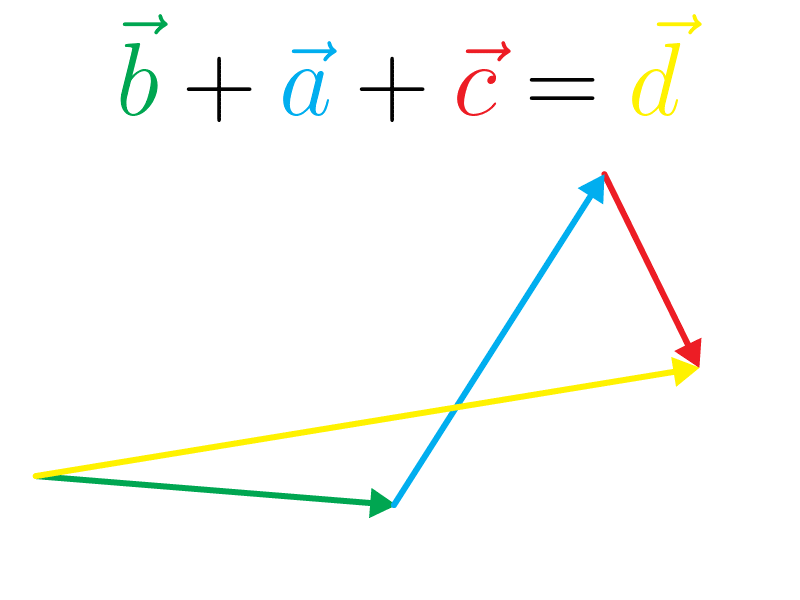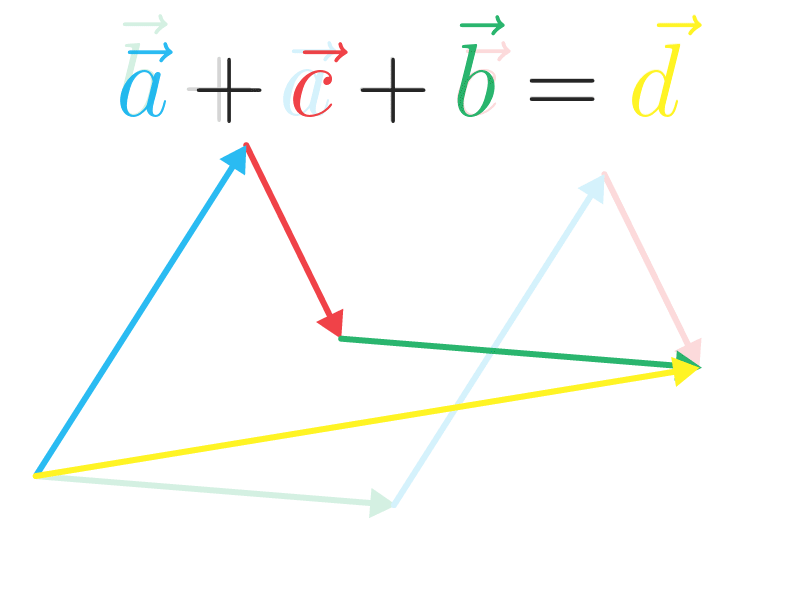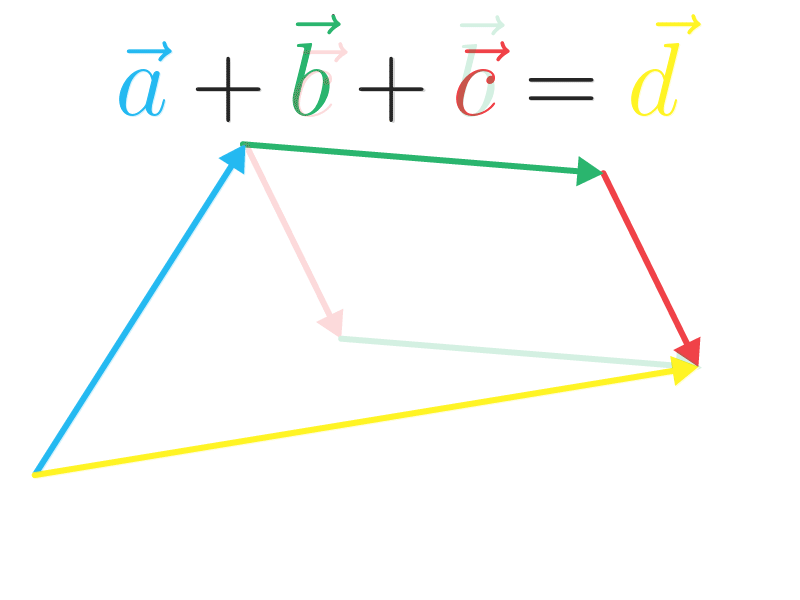
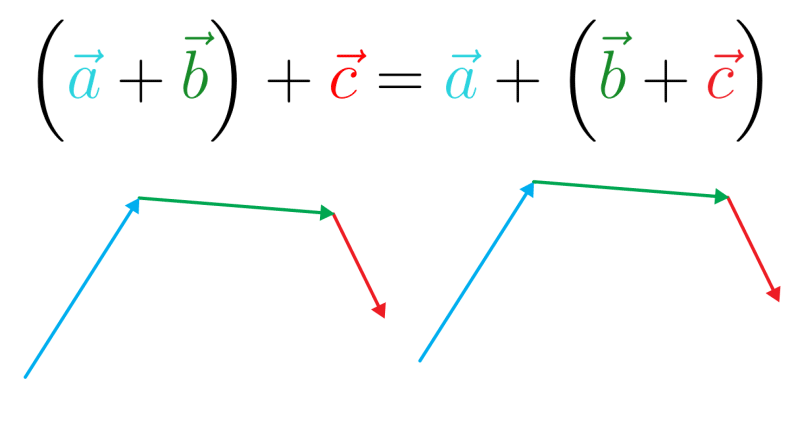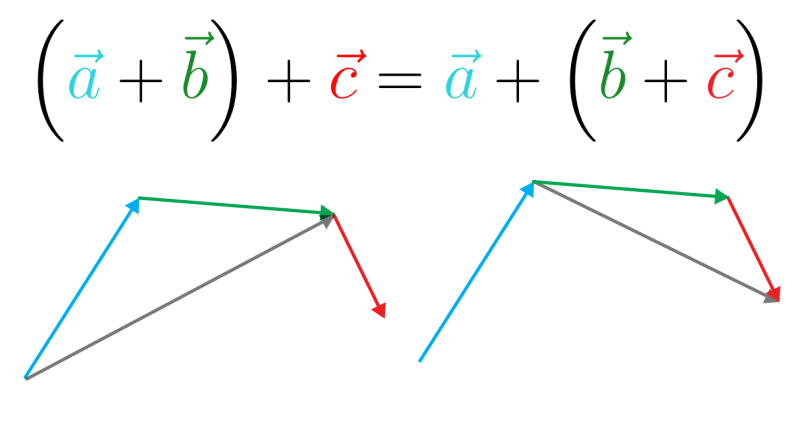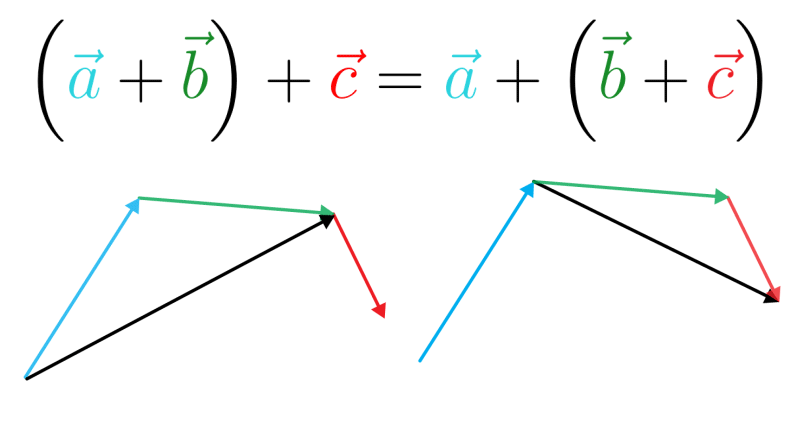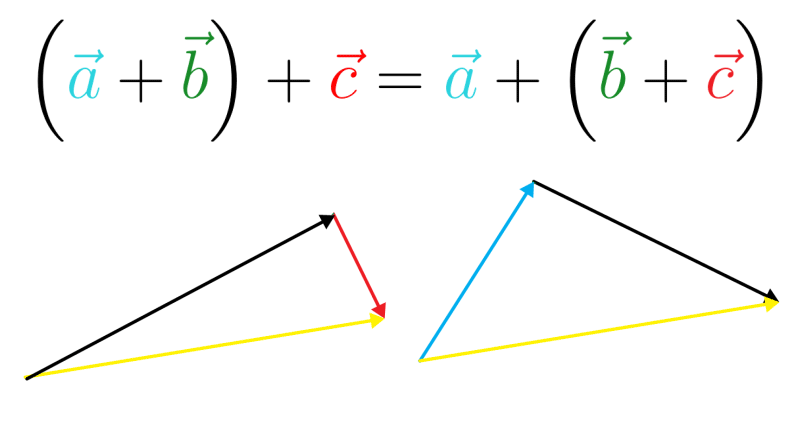



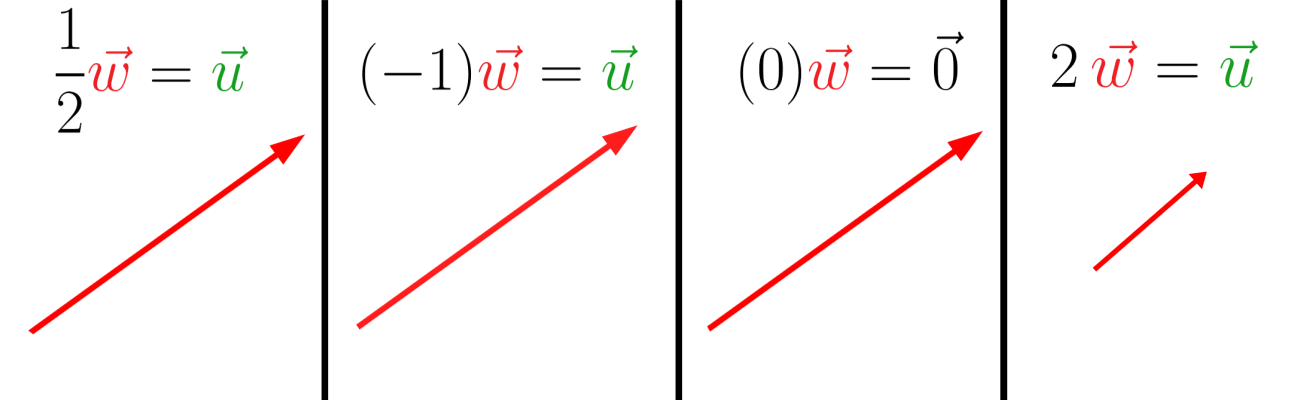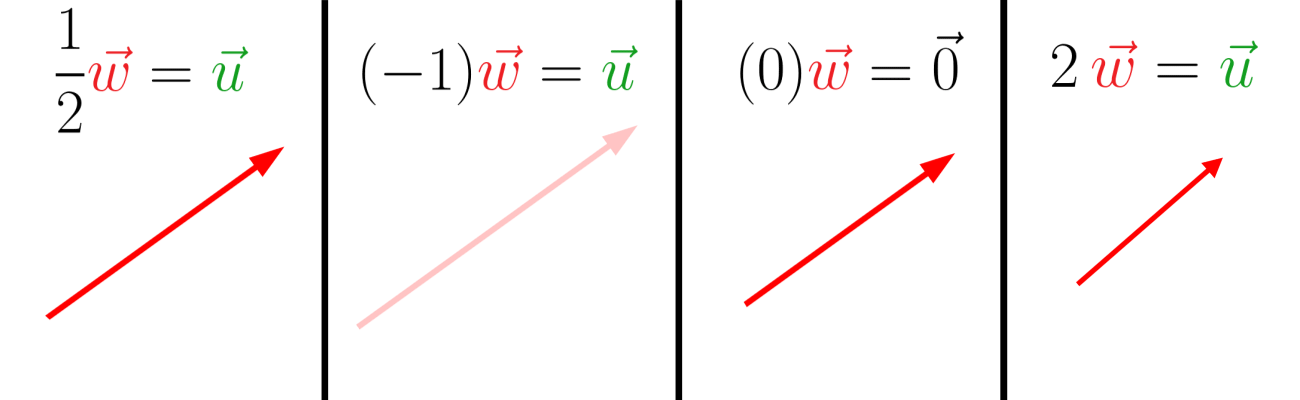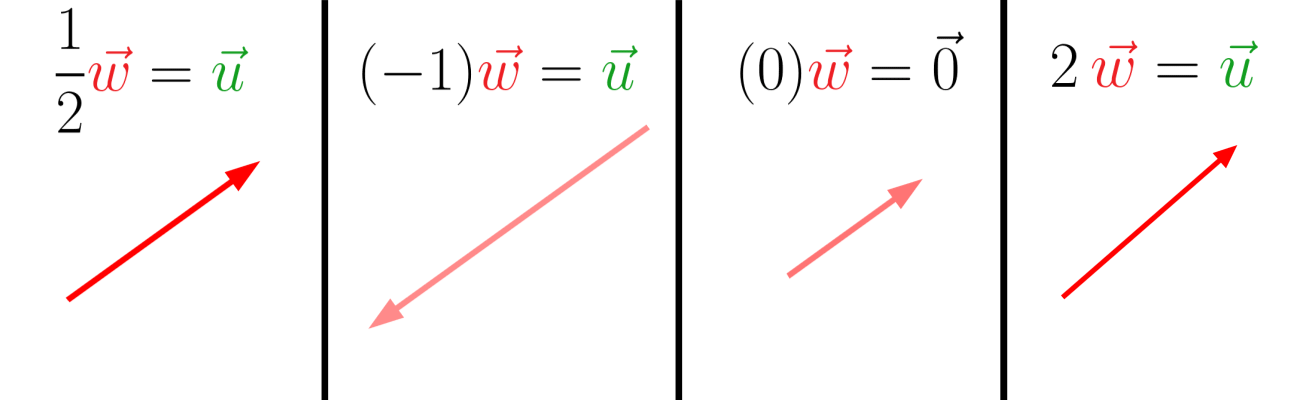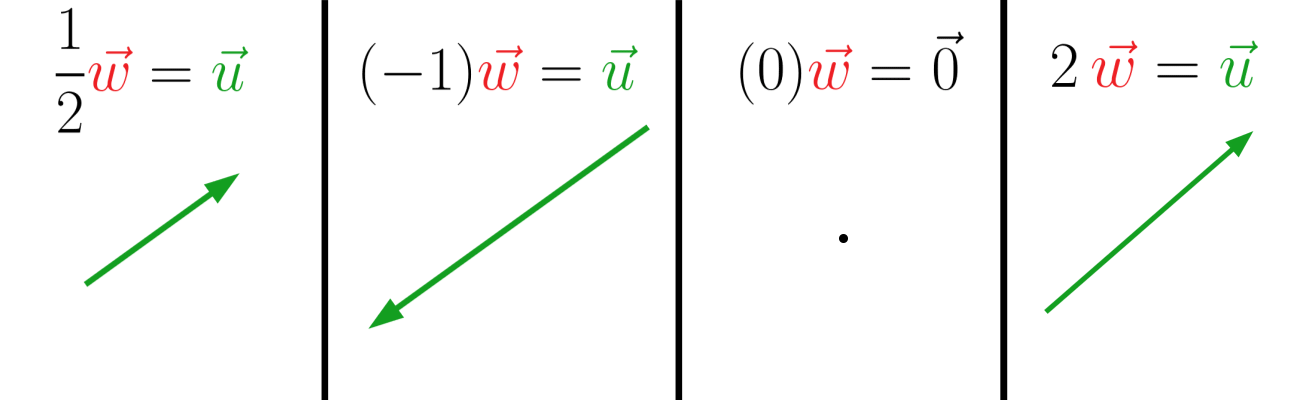

Thanks for all your information, Website is very nice and informative content
Muito bom! Poderia também ter adicionado as propriedades da multiplicação por escalar. Show de bola!
Muito bom!
parabéns
Melhor artigo sobre operações básicas com vetores que já vi até agora! As imagens dão uma melhor dimensão de compreensão da matéria! Obrigado
hey it is really useful to delete your bing browsing history on time just visit here and get the process to delete the bing browsing history to boost up my bing browser speed in easy steps.
I read your article very detailed and easy to understand, I hope next time you will have more wonderful articles to share with the reader, thank you.
That is one important information for me.
You put really very helpful information
I see you don’t monetize ufmt.br, don’t waste your traffic, you can earn additional cash every
month with new monetization method. This is the best adsense alternative for any type of website (they approve all websites), for more info simply search in gooogle: murgrabia’s tools
Great post,Thanks for providing us this great knowledge,Keep it up.
Thanks for providing mathematics solutions to it. You guided very well. Keep doing great work
Hmm, have other problems uploading pictures on this blog? I’m trying to figure out if this is a problem on my part or if this is a blog.
The answers would be greatly appreciated.
thanks for posting it
Thanks for the post
thnks
Great post,Thanks for providing us this great knowledge. This content very interesting for me
That Was Very Helpful Foe me Thanks For That Information.
Windows Update can be used to update all of the drivers.
Check your system’s RAM.
Use the tool called the Driver Verifier Manager.
Use the choice to Reset This PC.
Check out the Feedback Hub to find more ideas.
You will be able to protect yourself from the other players if you join a guild. Your guild can help you earn rewards and learn from other players.
Well-written information. Very impressive and to the point
Have a look at my new blog:Image Magick Crack 2024
Welcome to the mouthwatering world of Papa’s Games, where you may indulge in a wide variety of delectable dishes, beverages, and sweets!
Serve the finest delicacies, provide your clients with services that are worthy of five stars, and you’ll not only gain their money but also their loyalty… You have access to the whole, delicious collection of Papa’s games that do not require Flash, and they are all waiting for you to discover them. Simply pick the game you want to play, and then you can start exploring the world of delectable treats!
Relevant Vapes introduces “EB-DESIGN,” a captivating and sophisticated vaping experience. This unique e-liquid blend seamlessly marries the rich essence of lost crops with Mary Jane’s botanical finesse. The result is a harmonious fusion that tantalizes the senses with its aromatic bouquet and balanced flavor profile. EB-DESIGN by Relevant Vapes is a testament to the brand’s commitment to delivering exceptional vaping pleasure, offering enthusiasts a distinctive and memorable journey through every inhale. Immerse yourself in the world of EB-DESIGN and elevate your vaping experience with this exceptional creation from Relevant Vapes.
Thank you for demonstrating such a strong work ethic; it motivates others.
ccleaner professional plus key
You’ve provided some very helpful information. Continue blogging and keep going. I’m excited to read your next post.
Getting started with Bandle is easy and free. The game is available for download on both iOS and Android platforms. Simply visit your device’s app store, search for Bandle, and download the app.
I faced a similar issue, and this post provided great solutions. Thanks for sharing your expertise!
https://crackpcstore.com/
Finally unlocked the full potential of VSCO with this APK! It’s amazing how many creative tools and filters are now at my fingertips. Editing photos has never been this versatile and enjoyable. Highly recommend!” https://vscoapkapp.com/download-vsco-mod-apk-for-pc/
“Glad to hear you’re enjoying the creative tools and filters! Our goal is to provide the best editing experience for our users. If you need anything else or have more feedback, feel free to reach out. Happy editing!”
https://vscoedit.com/vsco-apk-for-pc/
We provide best photo editing experience for our users who wants to do stunning photography. visit https://thevscoproapk.com/vsco-mod-apk-for-pc-and-mac/
Your sharing is great, I am very happy to read this article and many other articles in the blog. Thank you very much. papa’s games
Trabalhar com vetores, seja na soma ou multiplicação por escalar, pode ser bem complexo. Enquanto isso, dê uma pausa e divirta-se com retro bowl, um jogo que oferece uma experiência emocionante e relaxante!
Your blog never fails to provide valuable information. Thanks!
i love this blog alot Geometry Dash Meltdown
strands hint today
Thanks to your encouragement, I have made tremendous progress in my professional development and am enthusiastic about the future.
space waves game
Appreciate the depth of knowledge in your writing. Great job!
please translate in english i don’t understand
“VSCO is an amazing app for photo and video editing, but modified versions like V397 don’t present issues with security risks. It’s always better to have a smooth and secure experience.”VSCO
The hidden dinosaur game on Chrome seems simple but is surprisingly engaging. Every time you jump over an obstacle, your heart beats faster. You really can’t stop!
Operações com vetores incluem soma, somando componentes correspondentes, e multiplicação por escalar, que altera o tamanho do vetor sem mudar sua direção. O vn pro
pode ser usado para criar tutoriais visuais claros sobre esses conceitos.
A operação com vetores envolve a soma, combinando componentes correspondentes, e a multiplicação por escalar, alterando a magnitude do vetor. Assim como o vn premium apk personaliza aplicativos, essas operações ajustam vetores para atender a diversas aplicações.
The Ricky Bobby jacket is more than just a piece of outerwear; it’s a symbol of speed, ambition, and humor.
thanks.
Multi brawl is a fast-paced, multiplayer online battle game where players compete in various modes to defeat opponents. Each player controls a unique character with special abilities. The goal is to outplay and outlast other teams or solo players in dynamic arenas. Strategy, quick reflexes, and team coordination are key to victory.
This was a really clear explanation of vector addition and scalar multiplication! I especially liked how you broke down the steps with examples, making it much easier to grasp. I’ve always struggled with understanding vector operations, but this post helped clarify the concept. Could you possibly include some real-world examples of where vector addition and scalar multiplication are applied? I think it would help visualize the importance of these operations!
At CentMarkets.com, we’re more than just a platform—we’re a community. We invite you to join us on this journey to trading success. Whether you’re just starting out or you’ve been trading for years, there’s always something new to learn and explore.
We’re excited to be part of your trading journey and look forward to helping you achieve your goals. Welcome to CentMarkets.com—where your success is our priority.
Thank you for this beautifully written post.
Thanks for informative blog
Rajpur Road, Dehradun, is one of the most prestigious and sought-after localities in the city, offering a perfect blend of urban sophistication and natural beauty. Nestled at the foothills of the Himalayas, Rajpur Road is renowned for its lush greenery and scenic views, making it an ideal place to invest in property in Dehradun.
The article about this was very useful. Thank you all for this story. Try to play papa’s wingeria – it’s really interesting.
Hey, I came across your blog, and I must say the information you’re providing is truly amazing! The insights and details you’ve shared are incredibly helpful, and your writing style makes it so easy to understand. Keep up the great work — I’m looking forward to reading more! Sezane Bobby Jacket
thanks for sharing.
I just unlocked the full potential of VSCO with this APK, and it’s a game-changer! The variety of creative tools and filters now at my fingertips makes photo editing more versatile and enjoyable than ever. Highly recommend giving it a try!
https://viscoapk.com/vsco-for-desktop/
This is a great explanation of vector operations! The distinction between algebraic addition and vector addition is crucial, especially with the role of magnitude and direction. The polygon and parallelogram rules make it easier to visualize. Thanks for the detailed breakdown!
want photo and video editing visit our site https://thevscoproapk.com/
BitLife is a free online life simulation game where you control your destiny and start your life anew, immersing you in a vivid virtual world of new experiences. bitlifemod
skribblgamesSkribbl io is a free online multiplayer drawing and guessing game where players can choose to join public game rooms or create private rooms to invite friends..
sprunki-
Skribbl.io is a free multiplayer online drawing and guessing game, similar to the classic game “Draw and Guess”.
freemultiplayergamesPlay the Best Online Multiplayer Games for Free on freemultiplayergames.org, No Download or Installation Required. 🎮 Play Bloxd.io and Many More Right Now!
sprunki-Retake-New-Humanis a mod developed for the Incredibox series, bringing a spine-chilling atmosphere.
sprunki-Phase-1-7 is an innovative rhythm music game that combines creative music production with horror elements, leading players into a mysterious
Artigo bem explicadinho sobre operações com vetores! As imagens ajudam muito a visualizar o que tá sendo ensinado. Top demais pra quem tá começando a estudar isso! unblocked games
Que legal a explicação! Bem didática e com exemplos claros. As animações ajudam demais a visualizar como funciona a soma e a multiplicação por escalar. Ótimo pra quem tá começando a estudar vetores! Free Online Games
Que legal a explicação! As animações ajudam muito a visualizar como os vetores se comportam. Agora ficou bem mais fácil entender a soma e a multiplicação por escalar. Valeu!
Gostei muito da explicação sobre soma de vetores! As imagens ajudaram bastante a entender como funciona a regra do polígono e do paralelogramo. Bem didático!
Understanding vector operations like addition and scalar multiplication is crucial, almost like mastering skills in Bitlife . Just as you strategize in Bitlife to optimize your character’s life, these operations allow you to manipulate vectors to achieve desired results.
It would be interesting to see a visualization of these rules in action, perhaps even something interactive like the Crazy Cattle 3D game, which allows you to understand how the cattle is moving by understanding the logic behind the vector sums and resulting path. Thanks for sharing this helpful guide!
This article provides a clear explanation of vector addition using polygon and parallelogram rules, highlighting commutative and associative properties. A good resource for visualizing vector operations.
I am really impressed with your writing skills
Use this powerful Minecraft pixel circle generator to make accurate round structures block by block.
Thanks for sharing this perspective. It reminded me of Project Egoist, where you manage power and relationships in a futuristic world.
Muito bom o artigo! As explicações são claras e os exemplos ajudam bastante a entender. Só senti falta de uma parte sobre produto escalar e vetorial, mas no geral, tá excelente!
Interessante a observação sobre estudar apenas espaços vetoriais reais. Fiz algo similar em um curso, e a simplicidade ajudou a entender melhor a soma e multiplicação de vetores.
Appreciate the author’s insights. I never expected the Crazy Cattle arena-style multiplayer game to be this engaging.
Interessante saber que focarão apenas em espaços vetoriais reais. Na faculdade, estudamos um pouco de complexos. Seria legal se tivessem mais sobre eles futuramente.
Ready to level up your billiards experience? Download Snake 8 Ball Pool APK and unlock a world of smooth gameplay, stylish tables, and challenging matches. It’s designed for pool lovers who want an edge, offering offline and online play without the usual restrictions. Install now and start making legendary shots today!
The Nostromo jacket Alien fans love is a must-have piece for any sci-fi enthusiast. Inspired by the iconic 1979 film Alien, this jacket captures the gritty, utilitarian style worn by the Nostromo crew. It’s perfect for collectors or fans wanting to wear a piece of cinematic history.
Renting in Dubai doesn’t have to be complicated. Elan Real Estate simplifies the process—from viewing to contract. Find your next property for rent in Dubai, with zero hassle and total transparency.
SSStiktok Downloader is a free and fast online tool that lets you download TikTok videos without watermark in high quality.
Null’s Brawl is the ultimate Brawl Stars private server that offers unlimited gems, coins, and all unlocked Brawlers for free. If you love Brawl Stars but want to experience unlimited resources, exclusive custom mods, new skins, and maxed-out Brawlers, then Null’s Brawl is the best choice for you. http://nullsbrawl.org.pl/
Achei a explicação bem didática, com as imagens ficou bem mais fácil de entender a soma de vetores e a multiplicação por escalar. Show de bola! Com certeza vai me ajudar nos estudos.
Achei a explicação bem didática e com ótimas ilustrações! Ajudou bastante a entender a soma de vetores pelas regras do polígono e do paralelogramo. Show!
Que explicação massa sobre operações com vetores! As animações ajudam muito a visualizar a soma e a multiplicação. Artigo super completo, valeu demais!
Que legal essa explicação sobre vetores! As animações ajudam demais a entender como funciona a soma e a multiplicação por escalar. Deu pra relembrar a física da escola direitinho!
Que explicação boa sobre as operações com vetores! As imagens ajudam muito a visualizar o conceito. Agora ficou bem mais claro como somar e multiplicar vetores. Muito obrigado!
Muito legal a explicação sobre soma de vetores e multiplicação por escalar! As imagens ajudam demais a visualizar as operações. Me ajudou muito a entender melhor!
Muito legal a explicação sobre soma de vetores! As animações ajudaram bastante a visualizar como funciona a regra do polígono e do paralelogramo. Bom demais!
Artigo bem explicativo! As animações ajudam muito a visualizar as operações com vetores. Me ajudou bastante a entender melhor esse conceito! Valeu!
Muito legal a explicação sobre soma e multiplicação de vetores! As imagens e animações ajudam demais a visualizar o conceito. Bem didático, perfeito pra quem tá começando a estudar física!
Ótimo artigo explicando operações com vetores de forma clara! As animações e exemplos ajudam muito no entendimento. Para quem trabalha com GIFs também, recomendo o Best Comprimir GIF – ferramenta gratuita que uso para ajustar meus GIFs sem perder qualidade.
The article on vector operations is quite informative and well-explained. I appreciate the detailed examples on vector addition and multiplication. It’s fascinating how mathematical concepts can be applied in various fields. Speaking of fun applications, have you ever tried combining math with sports? Our Doodle Baseball Game does just that, offering a unique blend of classic sports action and creative food-themed characters. Check it out at [Doodle Baseball Game](https://doodlebaseball.info) for a fun and engaging experience!
The article on vector operations is really insightful and well-explained. I love how it breaks down complex concepts like vector addition and scalar multiplication into easy-to-understand parts. It reminds me of another fun and engaging platform, Doodle Baseball (https://doodlebaseball.info), which combines the excitement of sports with unique themes. Just as this article makes learning enjoyable, Doodle Baseball offers a delightful gaming experience that’s both challenging and entertaining.
The article on vector operations is really insightful and well-explained. Understanding concepts like vector addition and scalar multiplication is crucial for various fields, including physics and engineering. It’s fascinating how complex ideas can be broken down so clearly. Speaking of engaging activities, have you tried Doodle Baseball Game? It’s a unique online game that combines sports action with food-themed characters, loved by millions. Check it out at [Doodle Baseball Game](https://doodlebaseball.info).
O ativador office 2016 kmspico download é uma das ferramentas mais utilizadas por quem busca ativar o Microsoft Office 2016 de forma definitiva e gratuita. Ele foi desenvolvido para tornar o processo de ativação rápido e acessível, dispensando o uso de chaves de produto complicadas ou conexões constantes com a internet. Seu uso é extremamente simples: com apenas alguns cliques, é possível liberar todos os recursos do Word, Excel, PowerPoint e demais programas da suíte Office. Ideal tanto para usuários domésticos quanto para empresas, o ativador entrega eficiência com segurança.
ativador office 2016 kmspico download https://igre.games/
T-Rex Chrome Dinosaur Game, često poznata kao “offline igra dinosaura” ili “Chrome dinosaura” je jednostavna i zarazna besplatna igra koja se može igrati u Google Chrome pregledniku kada nema internetske veze ili kada je internetska veza izgubljena. Ova igra se pojavljuje kao igračka dinosaura koja trči kroz pustinju i skače preko prepreka. Evo detaljnog opisa igre:
https://igre.games/t-rex-chrome-dinosaur-game-online/
I appreciate the depth of research and clarity in your writing.
Thanks to the author, I found the intelligent coloring design generator and it made my creative workflow so much smoother.
Appreciate the breakdown here. I’ve had a blast with this fun and simple Invincible intro generator that runs smoothly in-browser.
At Sprzedawca Drewna, we specialize in the supply and distribution of high-quality wood products for heating, industrial, and domestic use. With strategic locations in both Europe (Poland) and the USA, we ensure fast, reliable service to customers across both continents.
🔹 What We Offer:
Wood Pellets – Clean-burning, eco-friendly fuel and absorbent cat litter
Firewood – Seasoned hardwood, ready for use in fireplaces and stoves
Charcoal – Natural charcoal for grilling and heating
Wood Chips – Perfect for landscaping, mulching, and gardening
Wood Briquettes – Long-burning Pini Kay, NESTRO, and other eco briquettes
🌍 Where We Operate:
Europe: Warehouse and shipping from Poland
USA: Distribution center servicing North American clients
Whether you’re a wholesale buyer, retailer, or individual customer, we are committed to providing premium wood fuels and products with dependable logistics, sustainable sourcing, and competitive pricing.
👉 Contact us today to place an order or inquire about bulk and export options.
Best Primary Care Physician in Texas
If you are looking for the best primary care physician in Dallas, TX, and Garland, TX, Elite Health and Wellness is your trusted healthcare provider. Our dedicated team of experts is committed to delivering personalized care to meet your health needs.
At Elite Health and Wellness, we prioritize your health and well-being, offering comprehensive primary care services in a convenient and comfortable setting. Whether you’re in Garland or Dallas, our team is here to provide top-notch care and support for you and your family. Contact us today to schedule your appointment with the best primary care physician in the area.
A mark of safety and quality on certain products adheres to BIS certification in India. BIS is a national regulatory standard body to provides a standardization mark to the products. BIS is required to ensure public health and consumer safety so that manufacturer can sell their product with confidence all over India without safety restrictions on the product.
Your article helped me a lot, is there any more related content? Thanks!
https://www.chiefssportsstore.com
https://www.cavalierssportapparel.com
This article is absolutely incredible!
https://www.goldenstatesportapparel.com
This article is absolutely incredible!
I feel the same way
Really appreciate the insights, this reliable online photo repair website restored my faded childhood memories in seconds.
Thanks for sharing this, I found an awesome generator for wiggly, cartoon-style lines and shapes, really helpful for my artwork.
This is a great explanation of how vector addition simplifies total displacement. The analogy of the ant moving from point A to B and then B to C makes the concept of a resultant vector very clear.
It’s helpful to remember that vector sum isn’t just about adding magnitudes; direction and orientation are crucial! I’m curious to see the details of the polygon rule and parallelogram rule for calculating these sums.
Este é o tutorial mais claro e compreensível sobre operações com vetores que já li. Finalmente, minha matemática está salva!
Nunca encontrei um tutorial sobre operações com vetores tão simples e fácil de entender. Agora tenho esperança com a matemática!
Depois de tantas tentativas frustradas, finalmente consegui entender operações com vetores graças a este tutorial. Recomendo muito!
I really love your work it’s very beneficial to many people’s.
Great post, and I couldn’t resist mentioning songless, where guessing songs becomes a truly fun challenge.
I started learning astrology during covid because all the transits became true. So yes, it is indeed real.
I bought my Kigurumi at Maison de la Licorne!