Produto Vetorial

Definição

A maioria das pessoas considera o produto vetorial um pouco mais difícil de se calcular do que o produto escalar. Isso provavelmente acontece pois, para erros não serem cometidos, essa operação requer um pouco mais de atenção.

Vamos aprender, então, de onde vem o produto vetorial, parte por parte.

Ao multiplicarmos dois vetores, o resultado será um terceiro vetor, daí o nome produto vetorial. Mas como descobrimos o módulo, sentido, e a direção desse vetor resultante? É importante a compreensão desses tópicos para se ter um aprendizado mais completo.

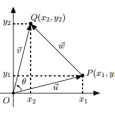
Bem, o módulo do produto vetorial é equivalente à área do paralelogramo formado pelos dois vetores. Vejamos o seguinte exemplo:

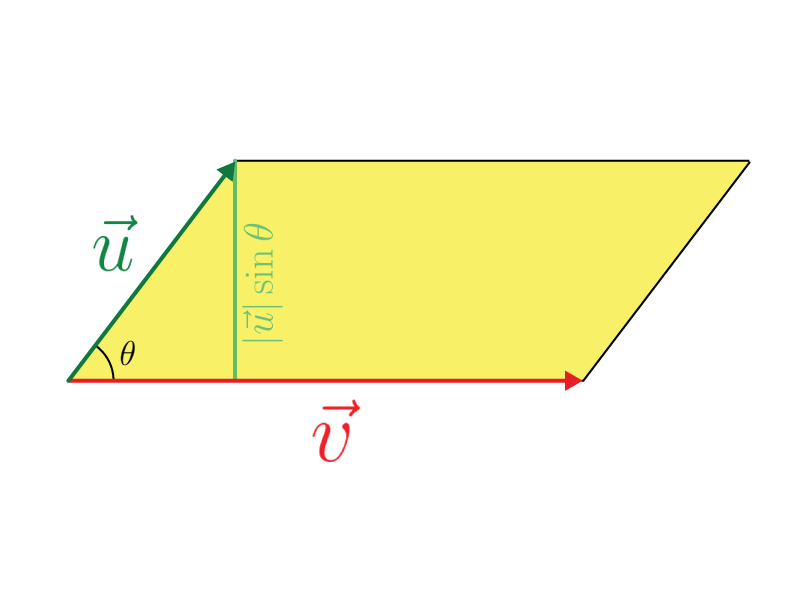
O módulo do vetor u multiplicado pelo vetor v representa a área do paralelogramo formado pelos próprios vetores u e v.

Temos que a altura desse paralelogramo é igual a $\left | \vec u \right | \sin \theta$ e a base igual a $\left | \vec v \right |$. E sabemos que, para calcular a área de um paralelogramo devemos fazer base x altura. Logo, o módulo do produto vetorial entre $\vec u$ e $\vec v$ é dado por: $$\left | \vec u \right |\left | \vec v \right |\sin\theta=\acute{A}REA$$

Ao contrário do produto escalar, que pode ser definido num plano cartesiano, o produto vetorial poderá ser definido apenas no espaço.

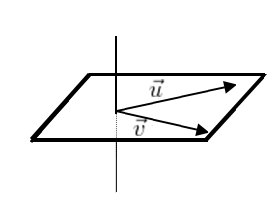
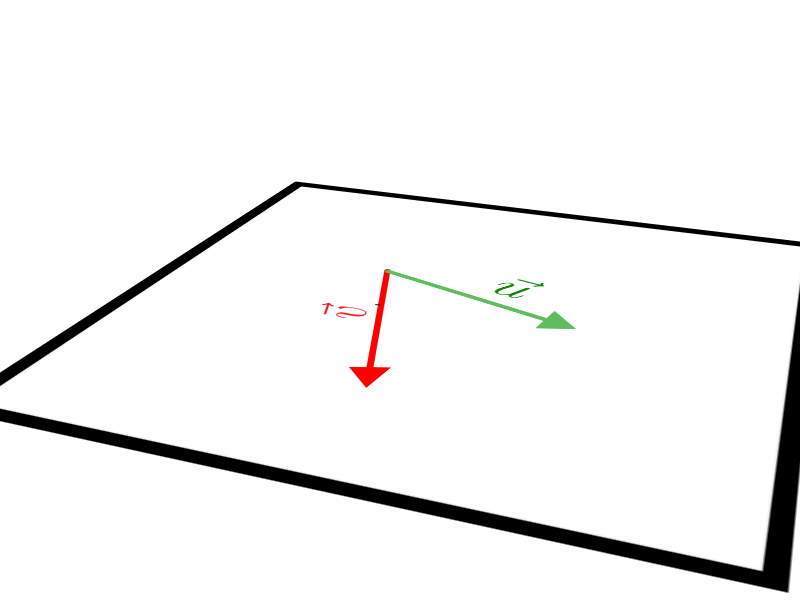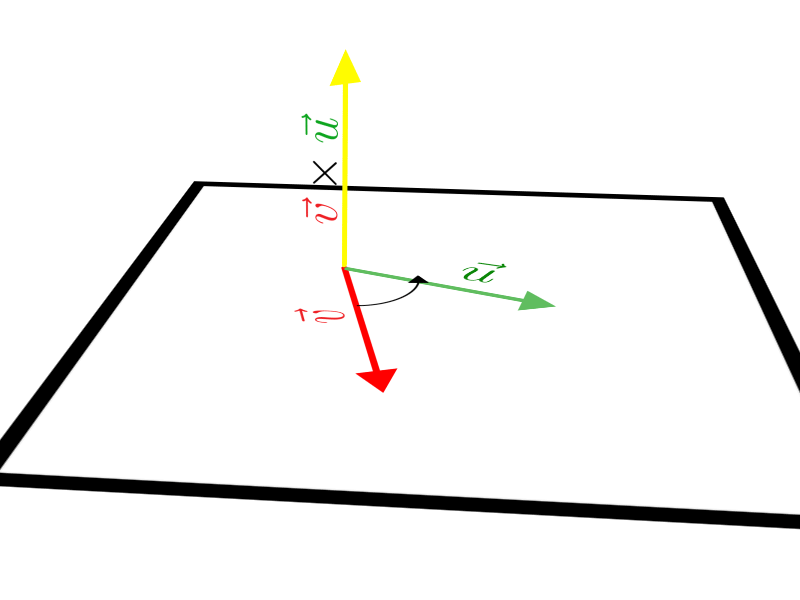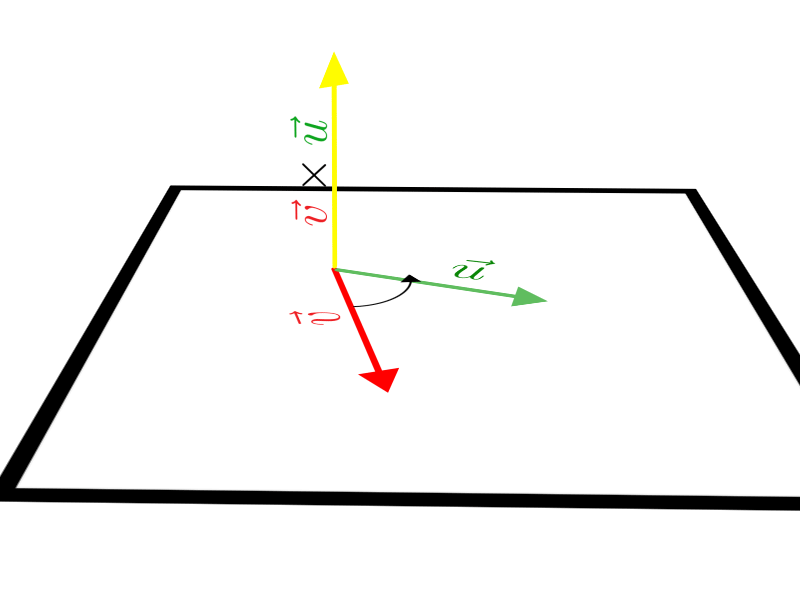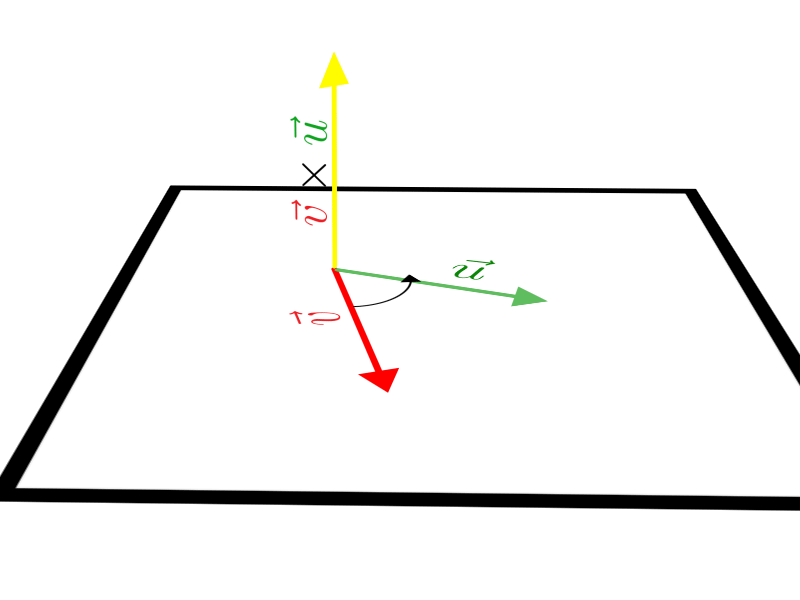
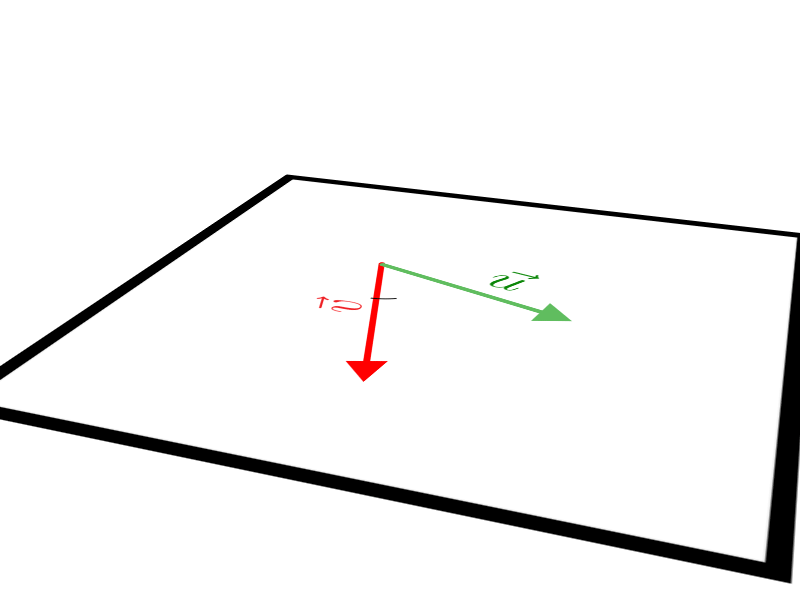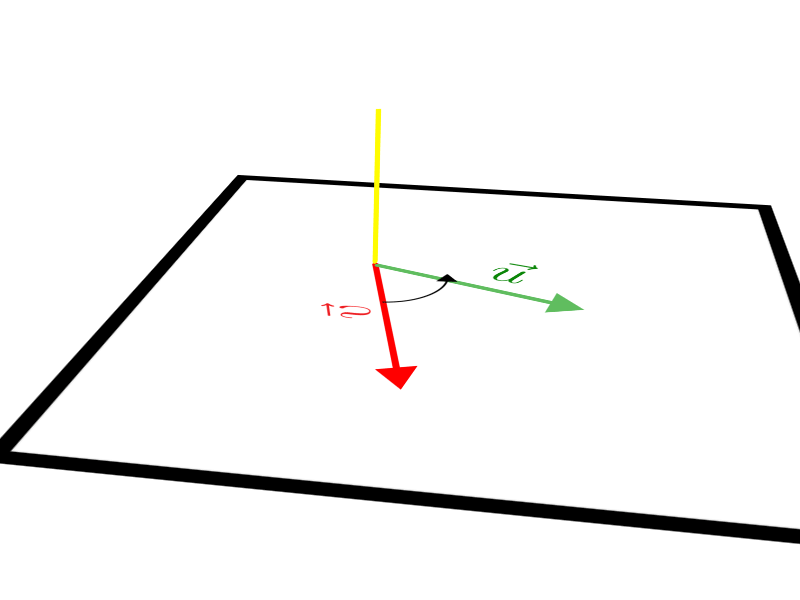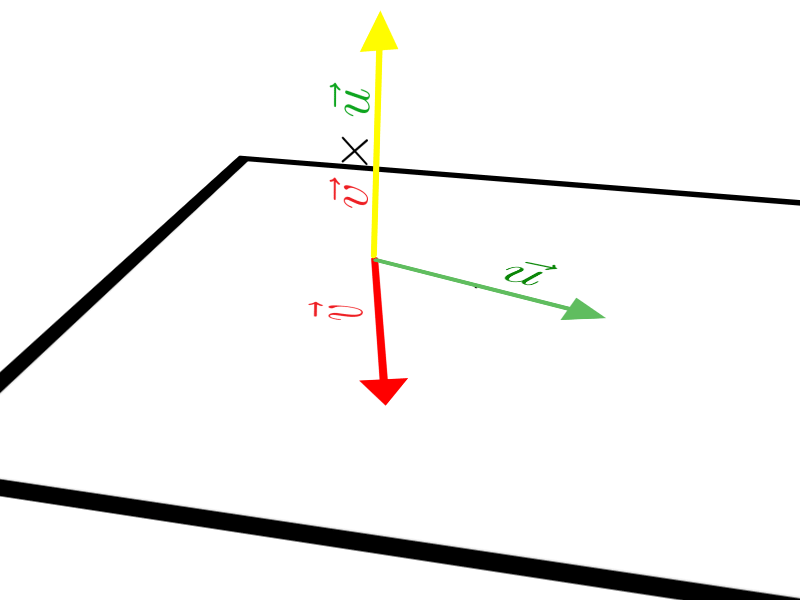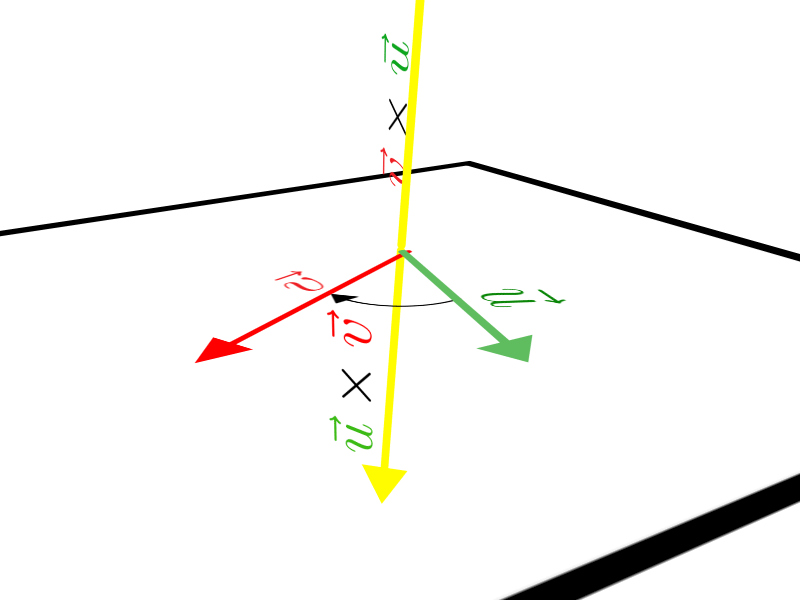
A direção do vetor resultante é dada pela reta perpendicular ao plano. Toda vez que traçamos vetores no espaço, podemos dizer que uma reta perpendicular ao plano definido, por exemplo, por $\vec u$ e $\vec v$, “automaticamente aparecerá” passando pela origem comum. Logo, essa reta sempre nos dará a direção do vetor que encontramos. Observe:

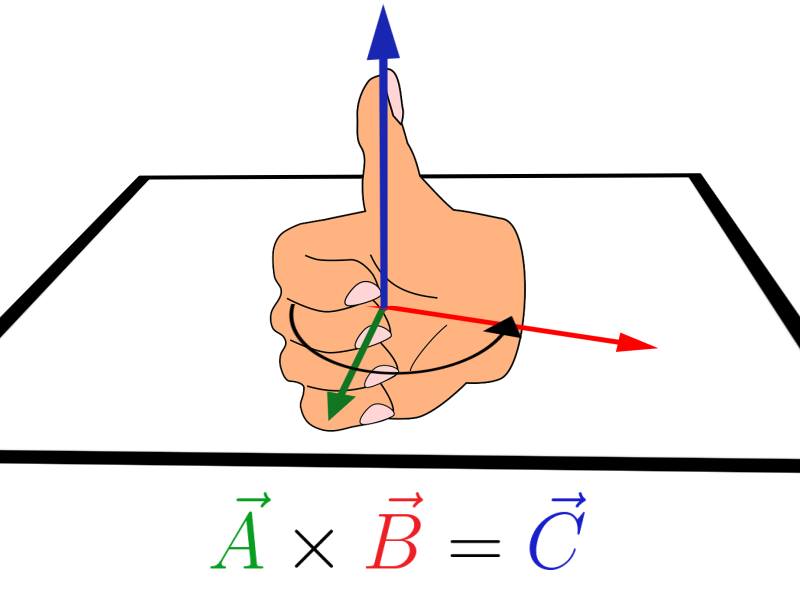
Precisamos saber também o sentido desse vetor resultante, que pode ser encontrado através de uma regra denominada “regra da mão direita”:

“Com o dedo indicador, alinha-se a mão direita com o primeiro vetor, dobra-se o dedo médio, alinhando-o com um segundo vetor, como representado na figura abaixo. O sentido do vetor fica definido de acordo com o fechar da mão, e a direção é a mesma da reta perpendicular ao plano.”

Observe:

Para resumir, temos por definição que, para calcularmos o módulo do produto vetorial faz-se uso da seguinte equação: $\left | \vec v \times \vec u \right |= \left |\vec v \right |\left | \vec u \right |\sin \theta$. A direção do vetor resultante terá sempre a mesma direção da reta perpendicular ao plano definido por $\vec u$ e $\vec v$, e o sentido será dado através da regra da mão direita, apresentada acima.

Exemplo (Clique aqui)

O vetor $\vec u$ tem um módulo igual a 18 unidades e forma um ângulo de 90º com o vetor $\vec v$, que possui um módulo de 12 unidades. Qual o produto vetorial $\vec c = \vec u \times \vec v$?

O seno de 90º é igual a 1, então: $$ \left | \vec u \times \vec v \right |=(18)(12)(1)=216$$

Encontramos o módulo do vetor resultante $\vec c$. Mas, e a orientação, como encontrar? É exatamente para isso que fazemos uso da regra da mão direita: coloque os dedos da mão direita em torno da reta perpendicular ao plano de $\vec u$ e $\vec v$ de modo que seus dedos empurrem o vetor $\vec u$ na direção de $\vec v$; o seu polegar estendido fornece a orientação de $\vec c$.

Propriedades

Ao trabalhar com produto vetorial devemos nos lembrar de alguns detalhes, por exemplo: a regra comutativa não é válida, ou seja, o produto vetorial é anticomutativo. Preste atenção na animação:

Na animação podemos ver como a mudança de ordem na operação altera o vetor resultante.

Veja que, $\vec u \times \vec v$ tem o mesmo módulo e direção de $\vec v \times \vec u$, porém sentido oposto. Portanto: $\vec u \times \vec v =- \vec v \times \vec u$.

O módulo do produto vetorial só será igual a 0 quando um deles for vetor nulo ou se os dois possuírem a mesma direção:

Bibliografia e Pesquisas

“Fundamentos da Física; Mecânica; 1” – Halliday & Resnick
“Cálculo Vetorial e Geometria Analítica – Luiz Francisco da Cruz – Departamento de Matemática – Unesp/Bauru”
“Apostila – Vetores – UFAL”
Imagem (1): “Regras para determinar o sentido do campo magnético.” – donaatraente.wordpress.com

Sobre o Autor

Carolina Moura

Produto Escalar

por Carolina Moura em dezembro 2, 2015

Definição O produto escalar é a multiplicação entre dois vetores que tem como resultado uma grandeza escalar. Ele associa a dois vetores um número real. Tomemos os vetores e como exemplo. O produto escalar entre os dois vetores pode ser interpretado como o produto da projeção de em e o módulo de . Logo, o produto escalar entre e é definido […]

Olá Mundo.

por jbruno em maio 6, 2015

Venho dar as boas vindas a vocês, acadêmicos do Curso de física UFMT e a comunidade externa. Breve história. O Projeto nasceu em uma conversa de boteco entre 3 alunos do Instituto de Física – UFMT (Jefferson Bruno, Yuri Silva e Thiago Ganascini), em 10/09/2013. No dia 15/09/2013 o site foi aberto, de nome “Comando Estelar”, com o […]

comments