Observação: Embora iremos estudar a queda livre nas proximidades da superfície da Terra, vamos desprezar as forças de resistência do ar em nosso post.
Definição:
De forma simples e direta podemos dizer queda livre é o movimento resultante unicamente da aceleração provocada pela gravidade, quando a velocidade inicial é zero \(v_{0}=0 \).
A aceleração da gravidade é uma das formas de se verificar que a Terra exerce, sobre os corpos, uma força chamada “atração gravitacional” (trataremos desse assunto em breve).
Podemos calcular o valor da aceleração da gravidade usando a mecânica newtoniana, através da 2ª lei de newton e da expressão da força gravitacional.
A 2ª lei diz que a força resultante que age sobre um corpo deve ser igual ao produto da massa do corpo por sua aceleração
$$\vec{F}=m\vec{a}$$
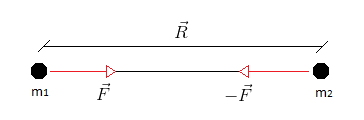
A expressão da força gravitacional entre duas partículas de massas m1 e m2 separadas pela distancia \( \left | \vec{r} \right | \)
$$\vec{F}=\frac{-Gm_{1}m_{2}}{\vec{R}^{2}} \frac{\vec{r}}{\left | \vec{r} \right |}$$
Nesta expressão, G é uma contante universal dada por \(G=6,674287×10^{-11} m^{3}kg^{-1}s^{-2}\)
(O sinal de menos indica que a força gravitacional é sempre atrativa).
Você pode se perguntar como podemos usar essa expressão, já que a terra não é uma partícula. Newton provou que uma esfera homogênea pode ser considerada uma partícula para fins do cálculo de força gravitacional. Claro que a terra não é uma esfera homogênea, mas suas irregularidades podem ser desprezadas numa primeira aproximação.
Como vamos utilizar esta aproximação também não vamos levar em conta as pequenas variações da gravidade, causadas pela rotação da terra e suas irregularidades topográficas.
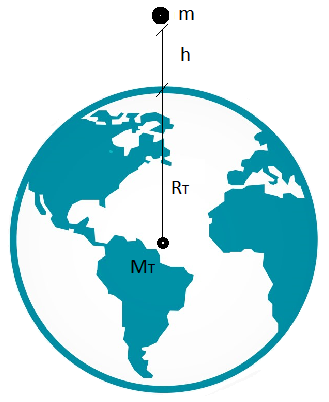
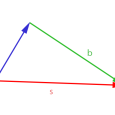
Vamos analisar em detalhe como surge a aceleração \( \vec{g}\).
A distancia a ser usada no calculo de g é \( \left | \vec{R} \right |=R_{T}+h \), onde o modulo de \( \left | \vec{g} \right |=g \). Assim sendo \(R_{T}\) sendo o raio da terra.
Utilizando a 2ª lei e a expressão da gravidade para calcular \( \vec{g} \)
Logo:
$$g=G\frac{M_{t}}{\left ( R_{T}+h \right )^{2}}$$
Observe um fato intrigante, a massa do objeto cancela na expressão acima. Ou seja, ao contrário da nossa intuição, qualquer que seja a massa do objeto que é largado, o \(g\) será o mesmo! Assim temos:
Porém podemos observar que o \(g\) não é independente da altura por causa do \(h\) na expressão. Ele na verdade diminui com a altura h! Mas porque os livros do ensino médio consideram g como uma constante? Isso ocorre porque para quenas alturas, h é desprezível em relação a \(R_{T}\).
Ou seja para \( h < < R \) (alturas pequenas), a aceleração gravitacional é praticamente constante.
$$g\cong G\frac{M_{T}}{R_{T}^{2}}\left ( constante \right )
\left\{\begin{matrix}
& M_{T}=5,9742×10^{24}kg & \\
& R_{T}= 6.378,1366 km
& \\
& G=6,674287×10^{-11} m^{3}kg^{-1}s^{-2} &
\end{matrix}\right.$$
Substituindo os valores de
Desta forma e muito adequado nós problemas encontrados em livros e provas do ensino médio \(g = 9.8 m/s^{2}. \). Porém para grandes alturas g cai de forma considerável.
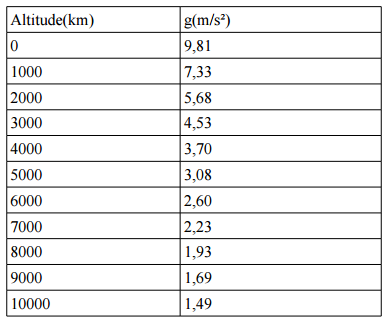
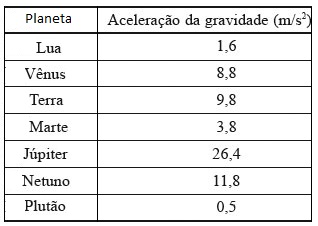
Veja a tabela abaixo e observe a variação de g para grandes alturas.
Como para os problemas que vamos abordar, o movimento nas proximidades da superfície da Terra, aceleração da gravidade é \(g = 9,8 m/s^{2}. \)
Cinemática do movimento (MRUV).
Dado um sistema de referência, o movimento é chamado retilíneo uniformemente variado (MRUV) quando a trajetória é uma reta e a velocidade varia linearmente com o tempo, isto é, a aceleração é constante.
A representação de um movimento pode ser feita através da fórmulas ou através do gráfico.
Cinemática da queda livre.
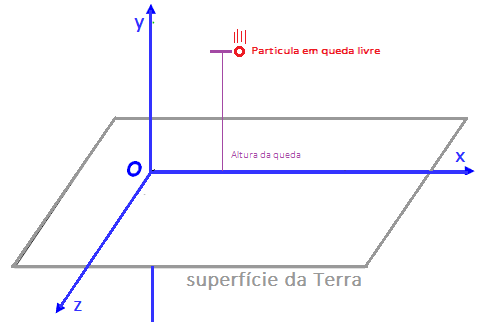
A partir de agora iremos tratar todo movimento de queda ou movimento retilíneo uniforme na direção do eixo y do sistema de coordenadas cartesianas, de queda livre.
____________________
Como aceleração do nosso movimento é constante, podemos utilizar as equações do MRUV:
$$v(t)=a\left ( t-t_{0} \right )$$
$$y(t)=y_{0}+\left ( t-t_{0} \right )v_{0}+\frac{a}{2}\left ( t-t_{0} \right )^{2}$$
Portanto o objeto é largado, assim \(v_{0}=0\). Logo as equações são rescritas com:
$$v(t)=a\left ( t-t_{0} \right )$$
$$y(t)=y_{0}+\frac{a}{2}\left ( t-t_{0} \right )^{2}$$
Assim se podemos iniciar a contagem do nosso cronometro no início da queda escolhemos \(t_{0}=0\). Logo:
$$v(t)=at$$
$$y(t)=y_{0}+\frac{at^{2}}{2}$$
Quando tratamos de corpos em queda livre, utilizamos o eixo dos y como referencial e a aceleração a é a aceleração da gravidade g e como falamos de um movimento de decida,a velocidade é negativa, pois obedece o sentido contrário à orientação do eixo y (referencial). Assim, sabendo que \(a=-g\), para \(g=9,8\) em relação a y, a equação do movimento pode ser reescrita da seguinte maneira:
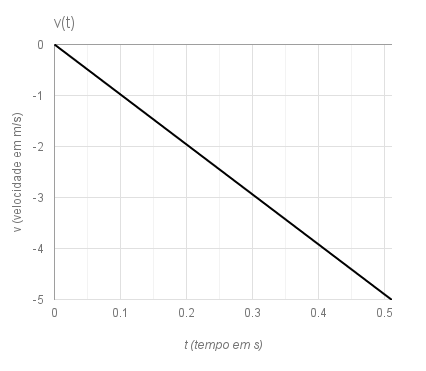
\(v(t)=-gt\) (equação horária da velocidade)
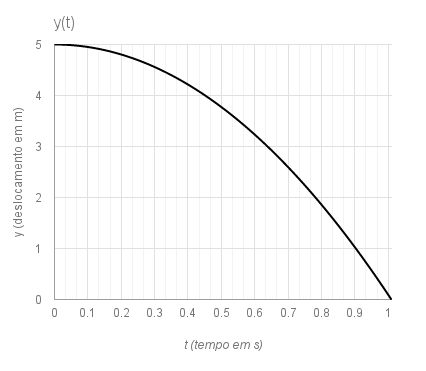
$$y(t)=y_{0}-\frac{gt^{2}}{2}$$
Essas expressões podem ser representados graficamente da seguintes formas:
( OBS: A velocidade é negativa porque a distância do corpo em relação à terra diminui com o tempo).
Obs.: Os gráficos acima foram produzidos usando os seguintes valores:
$$ g = 9,81 m/s^2 $$
$$ y_0 = 5 m $$
Mas como tratamos de corpos em queda livre a aceleração a é a aceleração da gravidade g e como falamos de um movimento de descida, a velocidade é negativa. Assim, a equação do movimento pode ser reescrita da seguinte maneira:
$$v=v_{0}-gt$$
Quando tratamos de corpos em queda livre, utilizamos o eixo dos y como referencial e a aceleração a é a aceleração da gravidade g e como falamos de um movimento de decida,a velocidade é negativa, pois obedece o sentido contrário à orientação do eixo y (referencial), assim, a equação do movimento pode ser reescrita da seguinte maneira:
$$y=y_{0}+v_{0}t-\frac{1}{2}gt^{2}$$
O tempo de queda livre, partindo do respouso (\(v_0=0\)) em \(y_0\) até a posição y é portanto:
\(t=\sqrt{\frac{2(y_{0}-y)}{g}}\) onde \(y_0\) é maior que \(y\) e a altura é dada por:
$$h=y_0-y$$
Assim com as equações horárias do movimento podemos saber a posição e a velocidade do objeto, em qualquer instante.
Vamos estudar a simulação:
Clique aqui para ver em uma nova janela
Podemos observar tal fenômeno de corpos com massa e dimensão variados, não afetam na queda de dois corpos, na a ausência do ar (no vácuo), no vídeo gravado pela BBC Two, onde o físico Brian Cox apresenta o experimento do fenômeno de dois corpos em queda livre no vácuo.
Você pode estar visitando o site oficial da serie para saber mais sobre este e outro experimento gravados nela. www.bbc.co.uk.
Ha também um vídeo gravado pela NASA na missão Apollo 15 (Moon Walk), onde comandante David Scott realizou uma demonstração ao vivo para as câmeras de televisão. Ele estendeu um martelo geológico e uma pena e deixou-os cair ao mesmo tempo. Porque eles estavam essencialmente no vácuo, não havia resistência do ar e a pena caiu na mesma taxa como o martelo, como Galileu tinha concluído centenas de anos antes – todos os objetos libertados juntos caem à mesma velocidade independentemente da massa. saiba mais no “15 Relatório Preliminar Ciência Apollo“.
Um objeto pesado (um martelo geológico 1,32 kg de alumínio) e um outro objeto de massa (a 0,03 kg pena) foram libertados simultaneamente. a partir de aproximadamente a mesma altura (aproximadamente 1,6 M) e foram deixadas cair sobre a superfície. Dentro da precisão da libertação simultânea, os objectos foram observados para submeter a mesma aceleração e atingir a superfície lunar simultaneamente, o que foi um resultado previsto pela teoria.



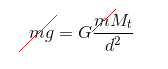

Hey as you know that most of the people usually facing the issue to open their saved folder in windows 10 operating system if they are new on it so for those here on our website you will get the most easiest tricks to open file explorer in windows 10 operating system.
Thanks for sharing the information. That is very helpful for increasing my knowledge in this field.
Thank s a lot for your advices, I may say that it works perfectly for all of my projects, for detailed info you may click here and check it by yourself.
Thanks for the post.
Get free Robux for free by visiting our blog.
I discovered the issue through your pen to be intriguing! Like myself, I think a lot of other people are curious about them.
Thanks for the wonderful information. This information is useful to all.
Wow, thank you so much for the fantastic information.
nice thank you for sharing useful information, keep posting.
vlone sale with a big discount in our vlone strore,hurry up to buy our vlone.
Great information. Thanks for sharing.
Thanks e-commerce au Maroc.
Thank you for giving this great information; please keep publishing.
wonderful piece. In my opinion, this is one of the best blog posts ever. I admire and am inspired by your work. That’s really kind of you.
In my opinion, this is without a doubt one of the most amazing blog posts that has ever been written. I admire and find motivation in the work that you do.
Your site was very useful for me, thank you.
Como aceleração do nosso movimento é constante, podemos utilizar as equações do MRUV:
v(t)=a(t−t0)
y(t)=y0+(t−t0)v0+a2(t−t0)2
ome interesting points in time on this article however I don’t know if I see all of them middle to heart. There is some validity however I will take maintain opinion until I look into it further. Good article ,
your post is quite clear and i can tell you know a lot about the subject
В 24fixboiler.ru мы предлагаем не только ремонт, но и профилактическое обслуживание водонагревателей. Регулярная чистка и диагностика продлят срок службы вашего оборудования, предотвратят поломки и сэкономят ваши деньги в будущем. Доверьте уход за своим водонагревателем профессионалам!
обслуживание водонагревателя
ремонт водонагревателей в москве
бойлер ремонт москва
Welcome to Yas Download’s online webpage. iPhone, iPad, iOS & Android video downloader with all features. You may download any video with this shortcut
Excellent article! I recently had an experience with this topic, and your insights really resonate with me.
https://macwinhub.com/photo-mechanic-crack/
I appreciate you disclosing this data. For the purpose of expanding my expertise in this area, that is really useful.
Awesome article! Thanks for making this complex topic so understandable.
Your blog is a great resource. Always appreciate your insights.
I’ve been using this software for a while now, and it’s become an essential part of my daily workflow.”https://crackcents.com/
I’ve been using this software for a while now, and it’s become an essential part of my daily workflow.
Top software
Data SGP merupakan rangkuman yang berisikan informasi mengenai hasil result dari pengeluaran singapore pools. Karena pasaran togel sgp terkenal membuat tingginya permintaan untuk menampilkan angka keluaran terbaru dengan cepat agar pemain langsung mengetahui pemenangnya.
The thoroughness of your analysis is truly impressive. wordle català
Thank you for sharing this! It’s incredibly helpful and exactly what I needed.
colorbox mustard
Thanks for this amazing content! It’s been a great help to me.
sprunki incredibox game
This is such valuable information! Thank you for taking the time to share it with us.
incredibox mustard game
I appreciate you disclosing this data.This is such valuable information!
sprunki game
This article was excellent. Very informative and well-explained.
I appreciate you disclosing this data.This is such valuable information!
https://pokemon-autochess.com/en/
Block Blast: Fill grids, strategize placements, and watch blocks vanish in satisfying bursts. Race the clock or relax endlessly. Rank globally, sync progress across devices. https://blockblast.space/
A math-music hybrid, Sprunkini lets players remix numbers 0-9 into Fourier-synthesized tracks. Horror variant injects Markov chain-driven tension via binary glitches. Master 47 interactions—prime power-ups, factorial combos—while teachers use it to demo modular arithmetic. Community spawns speedrun tiers and neural-net mods. Quantum superposition updates confirmed. https://sprunkigame.cam/
Clicker Sprunki 2: Quantum Evolution of Incremental Gaming reimagines idle play with Quantum Click Mechanics—each gesture warps particle fields in real-time. Strategize across 8 interconnected realities, where Cosmic Resonance Waves amplify resource yields. The Chrono-Strategic Compounding system rewards precision timing, while Sentient Bots craft meta-strategies beyond dev blueprints. Solve photon-forged puzzles in its 360° holographic UI, as Harmo-Click compositions mirror your neural rhythms. With 888% Data Redundancy and NFT-driven economies, it’s a cognitive gymnasium and esports arena. Laser-grid AR upgrades will merge clicks with light manipulation. https://squidki.us/
Abgerny’s Photonic Tablature System implants quantum muscle memory through 888% limb independence enhancement. Players navigate 12-dimensional string theory interfaces while maintaining 7-instrument entanglement. The Feedback Loop Algorithm warps stages into 16K holographic spaces with 888% reverb during quantum decoherence events. Compete in 8-limb anti-gravity battles or design light-speed solos using corrupted Sprunki Phase 9 melodies. Quantum Battle of Bands champions withstand 420G forces while syncing with 888 reality audiences. https://sprunkisquidki.online/
Pause to Play revolutionizes interactivity: every freeze-state lets players reprogram levels via menu sliders (gravity), checkboxes (parallel dimensions), and UI triggers (temporary platforms). Master momentum through multi-pause velocity chains, solve star-map puzzles in inventory screens, and conquer RGB synchronization challenges. The GMTK-recognized mechanics demand dual mastery—controlling characters mid-air while fine-tuning interface parameters. Pauses aren’t interruptions; they’re the core verb of this puzzle-platformer. https://pausetoplay.online/
Amanda the Adventurer turns a beloved cartoon into a cursed artifact. Players sift through decaying VHS tapes where Amanda’s lessons on friendship mutate into ominous prophecies, her world dissolves into glitch-terror, and her once-innocent frame distorts into abominations. The game’s dread spills into reality—her gaze tracks you, screen distortions mimic tape decay, and headphones can’t block her haunting voice. Progress locks her glitched face onto your browser, an ever-present watcher. A chilling exploration of analog media’s dark potential. https://amandatheadventurer.space/
Interesting explanation of free fall! The math is solid. It’s crucial to remember the air resistance caveat though, as that changes everything in real-world scenarios. Thinking about the trajectory reminded me of the Slope Game – where you feel the gravity constantly pulling! https://slopegamefree.io/
Bad Parenting is a psychological horror game that places players in the role of Ron, a child trapped in a house filled with unsettling secrets. The mysterious Mr. Red Face, a figure whispered about in childhood stories, lurks in the shadows, rewarding good children but hiding a much darker purpose. As Ron explores his home, he begins to uncover disturbing truths that challenge his understanding of reality. The game’s eerie soundscape, haunting visuals, and emotionally charged narrative create a horror experience that lingers long after the final scene. Is Mr. Red Face just a myth, or has he been watching all along? https://badparenting.us/
Create music with a comedic edge in Sprunki Parodybox, where humor and creativity come together. Build your own tracks using funny sound effects, animations, and customizable characters. Explore endless possibilities with community-made mods and enjoy crafting playful tunes that will keep you entertained. https://parodybox.party/
Sprunki 1996 reimagines 90s music production: drag sprites to mix lo-fi beats, warped synths, and arcade melodies. Its “lost software” aesthetic—pixel art, CRT filters, and cassette glitches—pays homage to underground electronic scenes. With new characters and intuitive controls, craft tracks that feel both vintage and fresh. https://sprunki1996.cc/
Step into the realm of Sprunki APT, a mod that elevates the Incredibox experience with spectacular visuals, relentless beats, and smooth animations. It transforms music into a battlefield where classic characters wage rhythmic wars, promising an unforgettable creative journey. https://sprunkiapt.com/
Find your beauty rank objectively with Am I Pretty. This AI tool analyzes facial traits, providing a 1-100 score and confidence rating. Use it for dating app prep, retail insights, or personal growth—fast, free, and confidential. https://amipretty.online/
Sprunki 100 er musikleg med en avantgarde-twist. Her blander du ikke bare beats – du skaber multimedieoplevelser med lysende animationer, ukonventionelle vokaler og bassystemer der ryster skærmen. En sand fest for sanserne, der gør musikteori til ren underholdning.https://sprunki100.com/
Redefine digital illumination with Lumina Brush AI. Apply volumetric fog, sharp shadows, or soft glows using intuitive brushes. Real-time previews, non-destructive workflows, and 8K exports ensure professional quality. Free access unlocks studio tools for everyone. https://luminabrushai.org/
From lyric drafts to full productions in 10 seconds: Diffrhythm uses diffusion transformers to maintain musical flow across 285-second tracks. Handles sparse vocals, MP3 artifacts, and genre-blending prompts. Open codebase invites tech-savvy creators to tweak its DNA. https://diffrhythm.us/
From fan mod to creative powerhouse: Sprunki Phase lets you drag-and-drop animated characters to compose dynamic beats. Experiment with the black hat’s secret modes for glitchy surprises or ambient textures. Cross-device sync, browser-based access, and endless replayability. No skills needed—just curiosity. https://sprunkiphase.me/
Click, drag, compose: Sprunki Mod Game transforms 19+ characters into musical tools. Born as a mod, now enhanced with black hat secrets. Free on Poki-supported platforms.
https://sprunkimodgame.org/
Are you searching for an exciting way to see new-people? Kismia is actually a popular connection application that intends to bring such as-oriented men and women with her.
Thanks for sharing this article! It offered a fresh perspective and gave me a lot to think about — really appreciate the depth and clarity.https://www.ailogogenerator.sh/
Que legal! Uma explicação bem detalhada sobre queda livre, desde a teoria até as fórmulas. Me ajudou a relembrar uns conceitos importantes da física. Show!
Que legal essa explicação sobre queda livre! Sempre tive um pouco de dificuldade em entender como a gravidade afeta os objetos em queda. Agora ficou bem mais claro com as fórmulas e os gráficos. Valeu!
https://crazycattle-3d.online/
Thanks for sharing the information. That is very helpful for increasing my knowledge in this field.
Que legal essa explicação sobre queda livre! Sempre tive dificuldade de entender como a altura influencia na aceleração da gravidade. Agora ficou bem mais claro! Valeu FÍSICA NAS NUVENS! personal loan
Awesome write-up! Simple, to the point, and full of value. I’m definitely sticking around for more. Accountants Preston
This reminds me of how we navigate our journeys on Earth. Just as physics offers equations to predict the motion of falling objects, tools like MapQuest provide us with precise directions and estimated travel times, helping us plan our routes effectively. Both rely on understanding and predicting movement—be it of objects in free fall or vehicles on the road.
This post is very simple to read and appreciate without leaving any details out Great work.